태야

동적 계획법이란?

어떤 문제를 풀기 위해 그 문제를 더 작은 문제들로 나누고, 작은 문제들에서 구한 해를 어딘가에 저장한 다음 활용해 문제를 해결하는 알고리즘 설계 기법이다. DP는 이름처럼 다이내믹한 프로그래밍이라는 거리가 멀다. 단순히 붙여진 이름일 뿐이라고 한다.

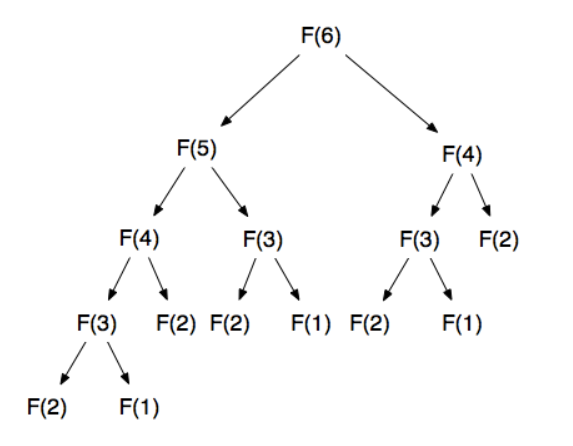
분할 정복 방식과 차이점

DP의 문제 접근 방식은 기본적으로 '분할 정복 알고리즘(Divide and Conquer)'과 비슷하다. 두 경우 모두 문제를 부분으로 나누어 각 부분 문제의 답을 계산하고, 이 값을 이용해 원래 문제를 해결하는 과정이다. DP와 분할 정복의 차이는 부분 문제로 나누는 방식에 차이가 있다. DP는 작은 문제들이 반복적으로 사용되며 (즉, 답이 바뀌지 않음) 반대로 동적 계획법은 작은 문제가 중복이 발생하지 않고 단순히 나누어 푸는 방법이다.

DP 문제의 해결 순서

1. 큰 문제를 작은 문제로 나눈다.

2. 재귀적인 구조를 활용할 수 있는 점화식을 만든다.

3. 작은 문제의 도출 값을 메모하고, 큰 문제를 풀어나갈 때 작은 문제가 반복되면 메모한 값을 이용한다. (Memoization방식)

DP의 조건

1. 작은 문제가 반복, 중복이 일어나는 경우

2. 같은 문제의 값은 매번 같다.

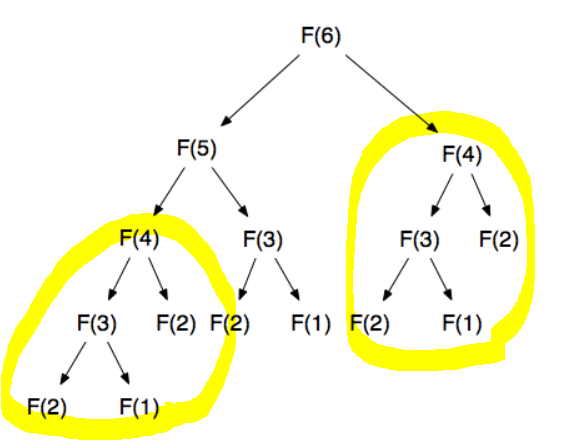
여기서 반복적으로 중복이 일어난 부분이 있다. 원으로 표시한 부분만 아니라 F(4)와 F(3)을 구하기 위해 모두 F(2)를 계산해야한다. 이런 식으로 매번 다 계산을 하면 시간적으로 비효율적이다. 그래서 DP방식을 이용해 메모이제이션을 통해 값을 활용해서 문제를 해결하면 훨씬 빠른 계산이 가능해진다.

<내 코드>

def binarySearch(M, tree):
    start = 1
    end = max(tree)

    while start <= end:
        leng = 0
        mid = (start + end) // 2

        for i in tree:
            if i >= mid:
                leng += i - mid

        if leng >= M:
            start = mid + 1
        else:
            end = mid - 1

    return end


N, M = map(int, input().split())
tree = list(map(int, input().split()))

sortTree = sorted(tree)
print(binarySearch(M, sortTree))

이분 탐색 알고리즘을 이용해서 푸는 문제다. 알고리즘만 알고 있으면 생각보다 간단한 문제였다. 같은 코드로 채점 했는데 pypy3는 588ms가 걸리고 python3는 2984ms 가 걸리면서 다소 큰 차이가 있었다. 

Python Code

def insert_sort(x):
    for i in range(1, len(x)):
        j = i - 1
        key = x[i]
        while x[j] > key and j >= 0:
            x[j+1] = x[j]  # 비교 값을 오른쪽으로 이동
            j = j - 1 # 앞쪽 값을 비교하기 위해 -1
        x[j+1] = key
    return x

삽입 정렬은 현재 값을 기준으로 앞쪽의 값들과 비교해 자기 자리에 삽입하는 정렬 알고리즘이다. 

삽입 정렬의 구체적인 알고리즘은 다음과 같다.

- 삽입 정렬은 두 번째 자료부터 알고리즘을 수행한다.

- 두 번째 자료(인덱스)부터 시작해 그 앞쪽의 값들과 비교해 삽입될 자리를 찾는다.

- 자리를 찾은 후 현재 값을 넣은 다음 나머지 값들은 한 칸씩 이동시킨다.(오른쪽)

- 세 번째 자료가 현재 값이 되고, 앞쪽 값인 첫 번째, 두 번째 값과 비교해 자리를 찾는다.

- 자리를 찾아 삽입되고 다른 값들은 옆으로 이동시킨다.

- 네 번째 값도 마찬가지로 왼쪽의 값들(1,2,3번째 값)과 비교해 삽입될 자리를 찾는다.

- 나머지 값들도 같은 방식으로 알고리즘이 수행된다.

위의 코드에서 보면 key가 선택된 값이 되고 j 인덱스가 왼쪽의 비교하는 값들이 된다.

j 번째 비교 값과 key 값을 비교했을 때 key가 작다면 j 번 값을 +1(즉 오른쪽으로 하나씩 이동) 시킨다. 계속 앞쪽의 값들과 비교해 비교 값들을 한 칸씩 오른쪽으로 이동시킨다.

만약 key 값이 더 크거나, 젤 앞의 값까지 비교가 끝나면 그 자리에 현재 값(key)을 넣어준다. 

삽입 정렬의 시간 복잡도

- 두 번째 값으로 시작 시 첫 번째 값과 비교 -- 1번

- 세 번째 값은 첫 번째, 두 번째랑 비교 -- 2번

- n-1 번째 값은 1, 2, 3,... , n-2 번째 비교 -- (n-2)번

- n 번째 값은 -- (n-1)번

즉, 1 + 2 + 3 + ... + n-2 + n-1 = n(n-1) /2 가 돼서, 시간 복잡도가 최악의 경우 O(n^2)가 된다. 최선의 경우는 자료가 다 정렬된 경우이고 이때는 시간 복잡도가 O(n)이 된다. 왜냐하면 각 자리의 값마다 왼쪽의 값 하나만 비교하면 되기 때문이다. 따라서 삽입 정렬은 n값이 커질수록 복잡도가 커져 알고리즘 성능이 떨어진다.

<내 코드>

case = int(input())
for _ in range(case):
	# n : 자료 개수 , m : 찾고자 하는 자료 위치
    n, m = map(int, input().split())
    imp = list(map(int, input().split()))
    temp = [0 for _ in range(n)] #리스트 표현식으로 0인 리스트 생성
    temp[m] = 1 # 찾고자 하는 m번째를 1로 표시
    cnt = 0

    while imp:
        if imp[0] == max(imp):
            cnt += 1
            if temp[0] == 1:
                print(cnt)
                break
            else:
                imp.pop(0)
                temp.pop(0)
        else:
            imp.append(imp[0])
            temp.append(temp[0])
            del(imp[0])
            del(temp[0])

- 중요도를 표시하는 imp 입력을 리스트로 만든다.

- imp 리스트와 비교하기 위한 temp 리스트를 만든다.

- imp[0]이 젤 큰 값인지 판단해, 아니라면 imp, temp 첫 요소를 뒤로 보내고 한 칸씩 땡긴다.

- imp[0]이 최댓값이면서 찾고자 하는 값이면 cnt 값을 출력하고 종료한다. 만약 찾고자 하는 값이 아니면 지우고 한 칸씩 땡긴다.

<내 코드>

from collections import deque
n = int(input())
nums = deque()

for i in range(1, n+1):
    nums.append(i)


def que():
    cnt = 0
    while(len(nums) >= 1):
        cnt += 1
        if(len(nums) == 1):
            return nums[0]

        if(cnt % 2 == 1):
            nums.popleft()

        elif(cnt % 2 == 0):
            nums.append(nums.popleft())


print(que())

처음에 deque 사용하지 않고 pop() 2개를 사용했더니 역시나 시간 초과가 났다.. 

카운트를 이용해 홀수, 짝수 순서에 따라 카드 제거 & 카드 뒤로 이동을 구현했다.