태야

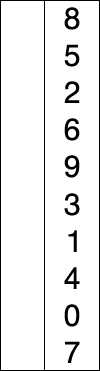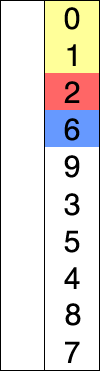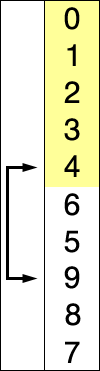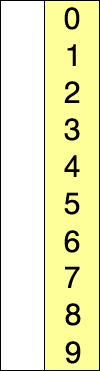
배열이나 리스트에서 각 원소에 대해 오른쪽에 있는 원소들 중 자신보다 크거나 같은(또는 보통은 '큰' 경우가 많지만, 변형으로 '크거나 같은' 조건을 쓰기도 한다) 첫 번째 원소를 찾는 문제다.

예시 문제 설명

예를 들어, 배열 A가 주어졌을 때A = [3, 5, 2, 7, 5]각 원소에 대해 오른쪽으로 이동하며, 처음 만나는 자신보다 크거나 같은 원소를 찾습니다.

- 3의 오른쪽에는 5, 2, 7, 5가 있는데, 처음으로 3보다 크거나 같은 수는 5입니다.
- 5의 오른쪽에는 2, 7, 5가 있는데, 2는 작으므로 건너뛰고, 다음 7은 5보다 크므로 7이 됩니다.
- 2의 오른쪽에는 7, 5가 있으므로 7이 첫 번째 큰(또는 같은) 수입니다.
- 7의 오른쪽에는 5만 있으나 5는 7보다 작으므로, 7은 오른쪽에 조건을 만족하는 원소가 없는 것으로 처리합니다.
- 마지막 원소인 5는 오른쪽에 아무 원소도 없으므로 조건을 만족하는 원소가 없습니다.

보통 조건을 만족하는 원소가 없을 경우 -1 또는 0 등 특정 값을 반환합니다.

단순하게 이중 반복문을 사용하면, 각 원소마다 오른쪽의 모든 원소를 확인해야 하므로 시간복잡도가 O(n^2)가 된다. 하지만 스택(stack)을 이용하면, 한 번의 순회로 각 원소를 효율적으로 처리할 수 있다.

스택을 사용하는 이유

• 스택의 특징
  
  • 스택은 후입선출(LIFO) 구조다. 이 특성을 이용하면, 배열을 한 번 순회하면서 "아직 답을 찾지 못한 원소들의 인덱스"를 스택에 저장해 두고, 새로운 원소가 들어올 때마다 이전 원소들과 비교하여 조건(큰 혹은 큰/같은)을 만족하는지 빠르게 확인할 수 있다.
• 시간복잡도
  • 각 원소는 스택에 한 번 push되고, 조건이 맞으면 pop되므로 각 원소가 스택에 들어가고 나오는 과정이 한 번씩 이루어집니다. 따라서 전체 시간 복잡도는 O(n)이 됩니다.

알고리즘 동작 과정

1. 초기화:
   빈 스택을 준비하고, 결과를 저장할 배열을 초기화한다. 결과 배열은 각 원소의 "다음 큰(또는 같은) 수"의 인덱스나 값을 저장할 수 있다.
2. 배열 순회:
   배열의 인덱스를 0부터 n-1까지 순회한다.
   • 현재 원소와 비교:
     현재 원소(A[i])가 들어왔을 때, 스택의 최상단에 있는 인덱스(예: j)를 확인한다.
     • 만약 A[i]가 A[j]보다 크거나(또는 크거나 같은) 하면, A[i]는 A[j]의 조건(다음 큰 또는 같은 수)을 만족하는 원소가 된다.
       따라서 결과 배열의 j번째 위치에 A[i] 또는 인덱스 i를 저장하고, 스택에서 j를 pop한다.
     • 이 과정을 스택이 비거나, 스택의 최상단 원소가 현재 원소보다 크거나 같은 조건을 만족할 때까지 반복한다.
   • 현재 인덱스 push:
     그 후, 현재 인덱스 i를 스택에 push한다.
3. 후처리:
   배열 순회가 끝난 후에도 스택에 남아있는 인덱스들은 오른쪽에 조건을 만족하는 원소가 없는 경우다. 이 경우, 결과 배열에 -1 또는 0을 기록한다.

Python 코드 예시

def next_greater_or_equal(arr):
    n = len(arr)
    result = [-1] * n  # 조건을 만족하는 원소가 없으면 -1로 처리
    stack = []  # 인덱스를 저장하는 스택

    for i in range(n):
        # 현재 원소 arr[i]가 스택의 최상단 원소보다 크거나 같으면 조건을 만족
        while stack and arr[stack[-1]] <= arr[i]:
            idx = stack.pop()
            result[idx] = arr[i]
        stack.append(i)
    
    return result

# 예시 실행
A = [3, 5, 2, 7, 5]
print(next_greater_or_equal(A))  # 출력 예: [5, 7, 7, -1, -1]

위 글을 요약하자면 다음과 같다.

• 문제: 각 원소에 대해 오른쪽에서 처음으로 자신보다 크거나 같은 원소를 찾는 문제.
• 단순 방법: 이중 반복문을 사용하면 O(n^2) 시간복잡도.
• 스택 사용: 스택을 이용하면 각 원소가 한 번씩만 처리되므로 O(n) 시간복잡도로 해결 가능.
• 핵심: 스택에 아직 답을 찾지 못한 원소의 인덱스를 저장하고, 새 원소가 들어올 때마다 조건에 맞는 이전 원소들을 처리.

DFS(Depth-First Search)와 BFS(Breadth-First Search)는 그래프나 트리 탐색에서 사용하는 대표적인 탐색 알고리즘이다. 두 알고리즘 모두 특정 노드를 방문하고, 그 노드와 연결된 다른 노드들을 탐색하는 방식으로 동작한다. DFS는 깊이를 우선으로 탐색하고, BFS는 너비를 우선으로 탐색한다.

1. DFS (Depth-First Search, 깊이 우선 탐색)

DFS는 탐색할 때 가능한 한 깊게 들어가는 방식으로 탐색한다. 즉, 한 경로를 따라 끝까지 가고, 더 이상 갈 곳이 없으면 다시 돌아와 다른 경로를 탐색한다. 이 방식은 재귀나 스택을 사용해 구현할 수 있다.

DFS 예시: 그래프 탐색

function dfs(graph, start, visited = new Set()) {
    // 현재 노드 방문 처리
    visited.add(start);
    console.log(start);

    // 현재 노드와 연결된 노드들을 재귀적으로 방문
    for (let neighbor of graph[start]) {
        if (!visited.has(neighbor)) {
            dfs(graph, neighbor, visited);
        }
    }
}
// 그래프 표현 (인접 리스트)
const graph = {
    1: [2, 3],
    2: [4],
    3: [5],
    4: [],
    5: []
}

dfs(graph, 1);  // 출력: 1 2 4 3 5

DFS의 시간 복잡도

• 시간 복잡도: O(V + E) (V는 노드 수, E는 간선 수)
• 그래프의 모든 노드를 방문하고 모든 간선을 처리해야 하기 때문에, 위와 같은 복잡도를 가진다.

2. BFS (Breadth-First Search, 너비 우선 탐색)

BFS는 탐색할 때 가까운 노드부터 차례대로 방문한다. 즉, 특정 노드에서 연결된 모든 노드를 먼저 탐색한 후, 그 다음 깊이의 노드들을 탐색한다. 이 방식은 큐(Queue) 자료 구조를 사용해 구현한다.

BFS 예시: 최단 경로 탐색

function bfs(graph, start) {
    const queue = [start]; // 탐색할 노드를 저장할 큐
    const visited = new Set(); // 방문한 노드를 저장할 집합
    visited.add(start);

    while (queue.length > 0) {
        const node = queue.shift(); // 탐색할 노드를 큐에서 꺼냄
        console.log(node);

        for (let neighbor of graph[node]) {
            if (!visited.has(neighbor)) {
                visited.add(neighbor);
                queue.push(neighbor);
            }
        }
    }
}

// 그래프 표현 (인접 리스트)
const graph = {
    1: [2, 3],
    2: [4],
    3: [5],
    4: [],
    5: []
};

bfs(graph, 1);  // 출력: 1 2 3 4 5

BFS의 시간 복잡도

• 시간 복잡도: O(V + E) (V는 노드 수, E는 간선 수)
• 모든 노드와 모든 간선을 한 번씩 방문하기 때문에 DFS와 마찬가지로 같은 복잡도를 가진다.

DFS와 BFS의 차이

• 탐색 방식: DFS는 깊이 우선으로 탐색하며, BFS는 너비 우선으로 탐색한다.
• 구현 방식: DFS는 재귀나 스택을 사용하고, BFS는 큐를 사용해 구현한다.
• 사용 사례:
  • DFS는 경로 탐색(예: 미로 찾기)나 백트래킹이 필요한 문제에 적합하다.
  • BFS는 그래프에서 최단 경로를 찾는 문제에 적합하다.

예시 문제

1. 미로 찾기

문제: N x M 크기의 미로가 주어질 때, 출발점에서 도착점까지 최단 경로를 찾으세요. 벽은 통과할 수 없으며, 상하좌우로만 이동할 수 있습니다.

// BFS
function shortestPath(maze, start, end) {
    const directions = [[0, 1], [1, 0], [0, -1], [1, 0]];
    const queue = [[start, 0]]; // [현재위치, 이동거리]
    const visited = new Set();
    visited.add(start.toString());

    while (queue.length > 0) {
        const [[x, y], distance] = queue.shift();

        if (x === end[0] && y === end[1]) return distance;

        for (let [dx, dy] of directions) {
            const newX = x + dx;
            const newY = y + dy;

            if (newX >= 0 && newY >= 0 &&
                newX < maze.length && newY < maze[0].length &&
                maze[newX][newY] === 0 && !visited.has([newX, newY].toString())
            ) {
                visited.add([newX, newY].toString());
                queue.push([[newX, newY], distance + 1]);
            }
        }
    }

    return -1; // 도착할 수 없는 경우
}

const maze = [
    [0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 0, 0, 0, 0]
];

console.log(shortestPath(maze, [0, 0], [4, 4]));  // 출력: 8 (최단 경로 거리)

2. 섬 개수 세기

문제: 2차원 배열에서 육지를 1, 바다를 0으로 나타내는 섬의 지도에서, 섬(연결된 1의 집합)의 개수를 구하세요.

// DFS
function numIslands(grid) {
    let count = 0;

    function dfs(grid, x, y) {
        if (x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] === '0') {
            return;
        }

        grid[x][y] = '0'; // 방문한 곳은 0 처리
        dfs(grid, x + 1, y);
        dfs(grid, x - 1, y);
        dfs(grid, x, y + 1);
        dfs(grid, x, y - 1);
    }

    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[0].length; j++) {
            if (grid[i][j] === '1') {
                count++;
                dfs(grid, i, j);
            }
        }
    }

    return count;
}

const grid = [
    ['1', '1', '0', '0', '0'],
    ['1', '1', '0', '0', '0'],
    ['0', '0', '1', '0', '0'],
    ['0', '0', '0', '1', '1']
];

console.log(numIslands(grid));  // 출력: 3 (3개의 섬)

1. 탐욕 알고리즘 이란?

• Greedy algorithm 또는 탐욕 알고리즘이라고 불림
• 최적의 해에 가까운 값을 구하기 위해 사용됨
• 여러 경우 중 하나를 결정해야 할 때마다, 매 순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행해서, 최종적인 값을 구하는 방식

2. 그리디 알고리즘으로 정답을 찾는 조건

1.  탐욕스러운 선택 조건(greedy choice proeprty)

2.  최적 부분 구조 조건(optimal substructure)

- 매번 탐욕스러운 선택을 해야 하며, 각각의 부분의 최적이 영원히 최적이 여야 한다.왜냐하면 그럴 경우 앞으로도 최적인 게 자명하기 때문이다.

즉, 한 번의 선택이 다음 선택에는 전혀 무관한 값이어야 하며 매 순간의 최적해가 문제에 대한 최적해여야 한다는 의미이다.

3. 탐욕 알고리즘의 한계

• 탐욕 알고리즘은 근사치 추정에 활용

• 반드시 최적의 해를 구할 수 있는 것은 아니기 때문

• 최적의 해에 가까운 값을 구하는 방법 중의 하나임

단, 그리디 알고리즘을 사용하면 매 선택이 그 순간에 대해서는 최적이지만 그걸 종합적으로 봤을 땐 최적이라는 보장은 절대 없다는 것을 명심해야 한다.

그리디 알고리즘에 따르면 매번 큰 값을 선택하면 4 - 9 - 12가 된다. 이것은 실제 최대 값이 아니라는 것을 알 수 있다. 실제로는 4 - 1 - 99를 따라가야 최대를 구할 수 있기 때문이다. 이처럼 그리디는 항상 그 상황에서는 최적이지만 종합적으로는 최적의 값을 도출하지 않는 경우가 발생한다.

동적 계획법이란?

어떤 문제를 풀기 위해 그 문제를 더 작은 문제들로 나누고, 작은 문제들에서 구한 해를 어딘가에 저장한 다음 활용해 문제를 해결하는 알고리즘 설계 기법이다. DP는 이름처럼 다이내믹한 프로그래밍이라는 거리가 멀다. 단순히 붙여진 이름일 뿐이라고 한다.

분할 정복 방식과 차이점

DP의 문제 접근 방식은 기본적으로 '분할 정복 알고리즘(Divide and Conquer)'과 비슷하다. 두 경우 모두 문제를 부분으로 나누어 각 부분 문제의 답을 계산하고, 이 값을 이용해 원래 문제를 해결하는 과정이다. DP와 분할 정복의 차이는 부분 문제로 나누는 방식에 차이가 있다. DP는 작은 문제들이 반복적으로 사용되며 (즉, 답이 바뀌지 않음) 반대로 동적 계획법은 작은 문제가 중복이 발생하지 않고 단순히 나누어 푸는 방법이다.

DP 문제의 해결 순서

1. 큰 문제를 작은 문제로 나눈다.

2. 재귀적인 구조를 활용할 수 있는 점화식을 만든다.

3. 작은 문제의 도출 값을 메모하고, 큰 문제를 풀어나갈 때 작은 문제가 반복되면 메모한 값을 이용한다. (Memoization방식)

DP의 조건

1. 작은 문제가 반복, 중복이 일어나는 경우

2. 같은 문제의 값은 매번 같다.

여기서 반복적으로 중복이 일어난 부분이 있다. 원으로 표시한 부분만 아니라 F(4)와 F(3)을 구하기 위해 모두 F(2)를 계산해야한다. 이런 식으로 매번 다 계산을 하면 시간적으로 비효율적이다. 그래서 DP방식을 이용해 메모이제이션을 통해 값을 활용해서 문제를 해결하면 훨씬 빠른 계산이 가능해진다.

 이분 탐색 알고리즘 - 파이썬

이분 탐색은 값을 비교할 때마다 찾는 값이 있을 범위를 절반씩 좁히면서 탐색하는 효율적인 알고리즘이다. 이분 탐색에서 중요한 것은 '이미 정렬된 데이터'에서 값을 비교하면 찾는다는 것이다. 따라서 순차 탐색처럼 처음부터 하나씩 하는 것이 아니라 정렬된 데이터에서 기준점을 잡고 반으로 줄여나가며 찾는 것이기에 훨씬 효율적이고 빠른 알고리즘이다.

이분 탐색은 실생활에서 '책'을 떠올리면 쉽게 이해할 수 있다. 우리는 책을 이용해 원하는 것을 찾을 때 첫 페이지부터 찾는 것이 아니라, 중간쯤 쪽수를 찾아 펼친 다음 범위를 좁혀나가며 계속 찾아나간다. 원하는 페이지가 펼친 페이지보다 뒤에 있다면 앞쪽은 찾을 필요 없이 바로 뒤쪽부터 찾게 된다.

예제

def binary_search(a, x):
    start = 0
    end = len(a)-1

    while start <= end:
        mid = (start + end) // 2
        if(x == a[mid]): 	# 원하는 값 발견!
            return mid 
        elif (x > a[mid]): 	# 찾는 값이 더 크면, 오른쪽으로 범위를 좁혀 탐색
            start = mid + 1
        else:			# 찾는 값이 더 작으면, 왼쪽으로 범위를 좁혀 탐색
            end = mid - 1
            
    return -1			# 찾지 못했을 때

a = [1, 4, 9, 25, 36, 49] # 정렬된 자료
print(binary_search(a, 36)) # 5
print(binary_search(a, 12)) # -1

Python Code

def insert_sort(x):
    for i in range(1, len(x)):
        j = i - 1
        key = x[i]
        while x[j] > key and j >= 0:
            x[j+1] = x[j]  # 비교 값을 오른쪽으로 이동
            j = j - 1 # 앞쪽 값을 비교하기 위해 -1
        x[j+1] = key
    return x

삽입 정렬은 현재 값을 기준으로 앞쪽의 값들과 비교해 자기 자리에 삽입하는 정렬 알고리즘이다. 

삽입 정렬의 구체적인 알고리즘은 다음과 같다.

- 삽입 정렬은 두 번째 자료부터 알고리즘을 수행한다.

- 두 번째 자료(인덱스)부터 시작해 그 앞쪽의 값들과 비교해 삽입될 자리를 찾는다.

- 자리를 찾은 후 현재 값을 넣은 다음 나머지 값들은 한 칸씩 이동시킨다.(오른쪽)

- 세 번째 자료가 현재 값이 되고, 앞쪽 값인 첫 번째, 두 번째 값과 비교해 자리를 찾는다.

- 자리를 찾아 삽입되고 다른 값들은 옆으로 이동시킨다.

- 네 번째 값도 마찬가지로 왼쪽의 값들(1,2,3번째 값)과 비교해 삽입될 자리를 찾는다.

- 나머지 값들도 같은 방식으로 알고리즘이 수행된다.

위의 코드에서 보면 key가 선택된 값이 되고 j 인덱스가 왼쪽의 비교하는 값들이 된다.

j 번째 비교 값과 key 값을 비교했을 때 key가 작다면 j 번 값을 +1(즉 오른쪽으로 하나씩 이동) 시킨다. 계속 앞쪽의 값들과 비교해 비교 값들을 한 칸씩 오른쪽으로 이동시킨다.

만약 key 값이 더 크거나, 젤 앞의 값까지 비교가 끝나면 그 자리에 현재 값(key)을 넣어준다. 

삽입 정렬의 시간 복잡도

- 두 번째 값으로 시작 시 첫 번째 값과 비교 -- 1번

- 세 번째 값은 첫 번째, 두 번째랑 비교 -- 2번

- n-1 번째 값은 1, 2, 3,... , n-2 번째 비교 -- (n-2)번

- n 번째 값은 -- (n-1)번

즉, 1 + 2 + 3 + ... + n-2 + n-1 = n(n-1) /2 가 돼서, 시간 복잡도가 최악의 경우 O(n^2)가 된다. 최선의 경우는 자료가 다 정렬된 경우이고 이때는 시간 복잡도가 O(n)이 된다. 왜냐하면 각 자리의 값마다 왼쪽의 값 하나만 비교하면 되기 때문이다. 따라서 삽입 정렬은 n값이 커질수록 복잡도가 커져 알고리즘 성능이 떨어진다.

재귀 호출은 함수가 자기 자신을 다시 호출하는 것을 뜻한다. 알고리즘 공부에 있어서 중요한 개념이므로 확실하게 공부해야 한다. 재귀 호출에서 중요한 것이 반드시 '종료 조건'이 있어야 한다는 것이다. 만약 종료 조건이 없으면 무한루프에 빠지기 때문이다.

재귀 호출의 일반적인 형태

def func(입력):
	if 입력 값이 충분히 작으면: #종료 조건
    	return 결과
    ...
    func(더 작은 입력 값)  	# 더 작은 값으로 재귀 호출
    ...
    return 결과

재귀 호출의 세 가지 요건

1. 함수 안에서 자기 자신을 다시 호출한다.
2. 재귀 호출할 때 인자로 주어지는 입력 크기가 작아진다.
3. 특정 종료 조건이 만족되면 재귀 호출을 종료한다. 즉, 종료 조건이 있어야 한다.

[예 제]

1. 1부터 n까지 더하기

def call_sum(n):
    if n <= 1:
        return n

    return n + call_sum(n-1)


print(call_sum(100))

함수 안에서 자기 자신을 계속해서 호출하는 방식으로 1부터 n까지 합을 구한다. 

2. 팩토리얼 구하기

def fact(n):
    if (n <= 1):
        return 1

    return n * fact(n-1)


print(fact(1))  # 1
print(fact(10))  # 10! = 3628800

종료 조건으로 n이 1과 같거나 작아지면 1을 리턴하게 해 마지막으로 1이 곱해지면서 결과를 리턴한다.

3. 최댓값 찾기

def find_max(nums, n):
    if n == 1:
        return nums[0]

    max_num = find_max(nums, n-1)

    if (max_num > nums[n-1]):
        return max_num
    else:
        return nums[n-1]


a = [17, 92, 18, 24, 35]
print(find_max(a, len(a)))  # 92

사실 리스트에서 최댓값, 최솟값을 구할 때 max(), min() 함수를 사용하면 쉽게 구할 수 있다.

 알고리즘, 자료구조 - 선택 정렬 

선택 정렬이란?

리스트 안의 원소들 중 최솟값을 찾아 리스트의 앞쪽으로 보내고, 그 뒤에 남은 원소들에 대해서 반복적으로 최솟값을 찾아 정렬하는 알고리즘이다. 간단한 알고리즘이지만 성능면에서는 느리기 때문에 좋지 않은 방식이다.

- 선택 정렬 알고리즘의 구체적인 개념

1. 첫 번째 원소를 선택, 그 뒤의 원소들과 차례대로 비교해 최솟값을 찾는다.

2. 찾은 최솟값을 첫 번째로 옮긴다.

3. 두 번째 원소를 선택, 3번째 원소부터 끝까지 비교해 최솟값을 찾는다.

4. 위의 과정들을 계속 반복한다.

위의 알고리즘 방식을 보면 코드상에서 2개의 반복문이 필요하고 이는 시간 복잡도 면에서 O(n^2)의 시간이 걸린다.

- 시간 복잡도

0번 요소: (n-1) 번 비교

1번 요소: (n-2) 번 비교

 ...

n-2번 요소: 1번 비교

n-1번 요소: 0번 비교

전체 비교 횟수는 0+1+2+3+...+n-2+n-1 = (n-1)(n-1+1) / 2 가 된다. n의 수가 커지면 결국 n^2이 큰 영향을 가지고 나머지는 무시할 수 있다. 따라서 시간 복잡도는 O(n^2)가 된다. 

예제

def select_sort(li):
    n = len(li)

    for i in range(0, n-1): #0번째~n-2번(뒤에서 2번째)
        min_idk = i
        for j in range(i+1, n): #비교하려는 값 뒤부터 끝까지 비교
            if(li[j] < li[min_idk]): # 비교하려는 값보다 뒤에 값이 작다면
                min_idk = j 		 
        li[i], li[min_idk] = li[min_idk], li[i] # 최솟값 위치 변경 

    return li


print(select_sort([2, 4, 5, 1, 3])) # [1, 2, 3, 4, 5]